The detector

The FOPI detector has documented the investigation of the fragments and the particles produced in central heavy-ion collisions. As suggested by the name - FOPI stands for 4pi; a synonym for the entire solid angle-this detector detects, identifies, and determines the momentum of all charged particles emitted in a heavy-ion reaction. The detector structure is shown schematically in the diagram. Based on the modular combination of different detector systems, the total assembly achieves its goal of covering the complete range of beam energies (0.1 - 2 GeV per nucleon) made available by GSI's SIS heavy ion synchrotron. The target is located within a superconducting coil, which produces a magnetic field of 0.6 Tesla. Charged particles within this field travel along curved paths before passing through the drift chambers (shown in yellow). These chambers register both the particle track and the energy loss sustained by the particle in its passage through the detector gas. The energy loss is dependent on the type of particle and its momentum in a characteristic way. Figure 1 gives an impression of the available information. This shows the signals ("hits") as squares in a plane normal to the beam axis. In addition, lines have been drawn through connected hits, which have been recognized by the automatic track-recognition of the event. Further on through the detector, the majority of the particles land in scintillation counters (shown blue in the diagram), with which their flight time from the target can be determined. The combination of different measurements enables the unambiguous identification of the particles.
The FOPI detector's potential ability to identify particles is, however, not restricted to charged particles. Although neutral particles do not themselves leave signals in the detector system, some of them can be recognized and reconstructed thanks to their decay. This interesting class of particles includes neutral particles containing a strange quark, such as the neutral kaon and the -particle. Due to their strangeness, they are relatively long-lived, decaying after a flight of several centimeters into charged particles, which leave tracks in the detectors. Two such decays, also from a nickel-nickel reaction at 1.93 GeV per nucleon, are visible in Figure 1. It can be seen that not all of the tracks originate from the same point. The point of intersection of the majority of tracks is the interaction point in the target. The other tracks are candidates for secondary decays. As the momenta and particle types are already known, the calculation of the invariant masses and comparison with the rest masses of the candidate particles enables the direct determination of which tracks belong together.
The FOPI detector can simultaneously detect all the charged and some of the neutral particles produced in a heavy-ion reaction. Global correlations among the particles are thus possible. Also known as collective effects, these correlations provide meaningful signatures for the material properties described above. Here, the common properties shared by the various particles emitted are sought in order to reveal the driving forces. Two recent results have attracted particular attention: collective expansion and directed sidewards flow at the highest energies, the latter of which provides interesting information, particularly in the case of strange particles, on interactions with the surrounding matter.
Figure 2 shows one example of the information available to physicists. Essentially, the momentum distributions of the particles are measured. Components in the directions normal to the beam axis are of particular interest, as they are first produced in the reaction. The figure shows spectra of the so-called transverse masses for the reactions nickel against nickel and gold against gold at 1 GeV per nucleon. The transverse mass is derived from the addition of the squares of the rest masses of the respective particle types and their transverse momentum. The spectrum falls off exponentially, although the slope parameters increase with increasing particle mass and system size. The spectra are plotted so that the slope corresponds exactly to the reciprocal of the temperature. Figure 2 could thus mean that the temperatures at which the different particles are produced increase with increasing mass. This hypothesis is ruled out since then the pions would have to be first produced in the reaction and thus would come from its coldest phase. The key to understanding the process lies in the linear dependence of the temperature on the mass of the particles. The mean kinetic energies per particle mass contain a common component for all particles, independently of whether the particle was first produced during the reaction or the constituents were already present before the start of the reaction. Similar observations have been made over a wide range of fragment masses at lower energies using the FOPI detector [1]. This behavior has been interpreted to mean that the observed fragments arise from an expanding flow of matter, from which they all carry the same velocity component into the detector. The magnitude of this collective velocity is astoundingly high. Quantitative investigations show that, as the strong interaction "freezes out," the matter is traveling with a mean velocity of one-third that of light. Naturally, since the energy bound up in the collective kinetic energy is not available to heat the matter, this has consequences for the temperature to which it is heated. Exact analysis for beam energies of 1 GeV per nucleon gives temperatures of 85 MeV, which corresponds to around 1012 degrees Celcius. Although the density is not directly accessible from the measurements, comparison of the spectra and the rapidity-density distribution (right-hand column, Figure 2) can be used with the predictions of so-called transport models to determine the change in the density over time and the maximum density reached. The rapidity is thus a measure of the velocity component along the direction of the beam. For heavy systems, an beam energy of 1 GeV per nucleon produces approximately double the density of the ground state, and can thus be used at the GSI's SIS heavy ion synchrotron to prepare the conditions specified in the introduction. Variation of the beam energy and of the projectile-target combination enables the region between one and 2.5 times normal density to be covered.
The most intensively discussed theme recently has been the question of how generated particles, in particular vector mesons and kaons, behave under conditions of high temperature and density. It would appear that the observed probabilities of production of the antikaons in particular can currently only described theoretically if it is assumed that particle masses are lower in-medium. Another window on possible "in-medium properties" of kaons is founded upon the directed sidewards flow discovered some fifteen years ago by the GSI/LBL group at the Bevalac. As nuclear matter is extremely difficult to compress, the particles attempt, so far as is possible, to get out of the way. In the case of not completely central collisions-the most probable sort, due to the geometry-the particles are collectively deflected from the collision axis and thus define a preferred direction, which, together with the beam direction, defines the so-called reaction plane. Figure 3 shows how this behavior is reflected in distributions. The momentum components normal to the beam direction are projected onto the reaction plane and then evaluated. This average value is plotted against the rapidity for the various particles. For protons, which are represented by the stepped, green histogram, it can be seen that the average value increases in line with the absolute value of the longitudinal velocity, i.e. the protons are preferentially emitted at a particular angle in the reaction plane. The highest matter density is to be found in this direction.
The resolutions possible with the FOPI detector can best be gauged using the mass distributions shown. There, the reconstructed masses are shown for singly-charged particles from the nickel-nickel reaction at 1.93 GeV per nucleon for the solid angle region of the central drift chamber and its surrounding time-of-flight detectors. In order to make the "strange" particles visible in particular, only tracks with momenta of up to 450 MeV/c and velocities of up to 20 cm/ns are accepted. The extremely good resolution enables the detection of negatively-charged kaons, for example, although they are only produced with a relative abundance of 10-4 per collision. This resolution is independent of the azimuth angle at which the particles are emitted, a fact of decisive importance for the measurement of the correlation of nucleons and kaons discussed in this article.
Due to the conservation of strangeness, at beam energies of less than 2 GeV per nucleon kaons are always produced together with -particles. The particles are thus produced at the same location, and interaction with the surrounding matter is responsible for all differences observed in the detector. It therefore follows from the distributions shown in Figure 3, that kaons are repelled from the areas of high baryon density, while -particles are drawn in to these regions. It should, however, be noted that K+-mesons, in contrast to the -particles, can leave the reaction volume relatively undisturbed-at least that is what the properties of the free particles seem to indicate. In the lower part of Figure 3, measurements are compared with calculations in which G.Q. Li and C.M. Ko [2] investigated both the free interaction and different versions of the "in-medium interaction" of kaons with the surrounding matter. In the simplest case, corresponding to the dotted line, the kaons should simply not notice the presence of the nucleons. A flow signal in the nucleon direction is to be expected in this case. If an interaction, which can be expressed by a potential, is taken into account, then according to intensity and type, there is agreement with the measured values. The case in which the lateral flow data are described corresponds to the phenomenon of reduced mass mentioned at the start of this section: an attractive scalar potential is required in order to compensate, at least partially, for the strongly repulsive vector potential. Within the context of chiral models, such scalar potentials have clearly-defined effects on the masses of a very wide range of particles.
In particular, these hypotheses lead to significant differences between K+ and K--mesons, both in the probability of production and in the flow characteristics. However, such investigations are considerably more difficult, as K--mesons appear less frequently. Such measurements are currently being undertaken, along with the measurement of more exotic, higher-mass particles, such as the -mesons. The first results on the flow characteristics of the antikaons appear to fit with the theoretical predictions of the "chiral" model. However, evaluation is not yet complete. The current FOPI experiment program is expected to produce additional interesting information on the character of the interaction in hot, compressed nuclear matter.
Symmetric nuclear matter.
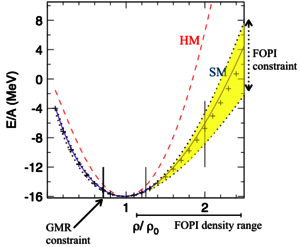
Using FOPI data on elliptic flow in Au + Au collisions between 0.4 and 1.5A GeV, constraints for the equation of state (EOS) of compressed symmetric nuclear matter have been extracted using the transport code IQMD by introducing an observable describing the evolution of the size of the elliptic flow v2 as a function of rapidity. This observable is sensitive to the nuclear EOS and a robust tool to constrain the compressibility of nuclear matter up to 3 times saturation density (Figure 4) [3].
It has been discovered that the elliptic flow of composite charged particles emitted at midrapidity in heavy-ion collisions at intermediate energies shows the strongest sensitivity to the nuclear equation of state (EoS), which has been observed up to now within a microscopic model. This dependence on the nuclear EoS is predicted by quantum molecular dynamics (QMD) calculations [3], which show as well that the absorption or rescattering of in-plane emitted particles by the spectator matter is not the main reason for the EoS dependence of the elliptic flow at midrapidity but different density gradients (and therefore different forces) in the direction of the impact parameter (x direction) as compared to the direction perpendicular to the reaction plan (y direction), caused by the presence of the spectator matter. The stronger density gradient in the y direction accelerates the particles more and creates therefore a negative v2. When using a soft momentum-dependent EoS, QMD calculations reproduce the experimental results. [4]
The deduced incompressibility modulus of symmetry nuclear matter has been found to range between 160 and 220 MeV using IQMD comparisons with FOPI data, and between 180 and 260 MeV using UrQMD [5].
Asymmetric nuclear matter
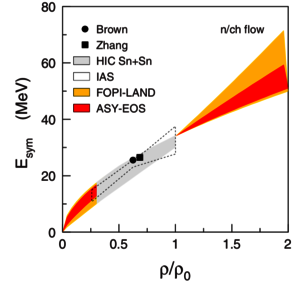
The combination of the LAND detector with the FOPI set-up allows measuring neutrons. The elliptic-flow ratio of neutrons with respect to protons or light complex particles in reactions of neutron-rich systems at relativistic energies has been found to be an observable sensitive to the strength of the symmetry term in the equation of state at supra-normal densities. The results obtained from the existing FOPI/LAND data for 197Au + 197Au collisions at 400A MeV in comparison with the UrQMD model favor a moderately soft symmetry term with a density dependence of the potential term proportional to (ρ/ρ0)γ with γ = 0.9 ± 0.4 [6]. This finding has been later confirmed and precised by the ASY-EOS experiment with γ = 0.9 ± 0.4 [7].
Deduced contraints on the symmetry term of the EOS are shown in Figure 5.
Astrophysical implications
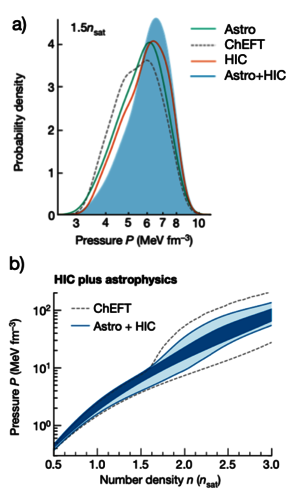
Combined altogether, EoS constraints of both symmetric and asymmetric nuclear matter allow infering the EoS of a neutron star, and therefore predicting its properties like mass-radius relation and tidal deformability.
Furthermore, it allows a better understanding of the dynamics of supernovae and neutron star mergers, complementary to gravitational wave and X-ray observations of those phenomena as show in Fig. 6, bridging this way macroscopic and microscopic collisions. [8][9]
[1] W. Reisdorf et al., Nucl. Phys. A 612, 493 (1997)
[2] G.Q. Li und C.M. Ko, Nucl. Phys. A 594, 460 (1995)
[3] A. Le Fèvre, Y. Leifels, W. Reisdorf, J. Aichelin, Ch. Hartnack, Nucl. Phys. A 945, 112 (2016) and W. Reisdorf et al. (FOPI Collaboration), Nucl. Phys. A 876, 1 (2012)
[4] A. Le Fèvre, Y. Leifels, C. Hartnack, and J. Aichelin, Phys. Rev. C 98, 034901 (2018)
[5] Yongjia Wang, Chenchen Guo, Qingfeng Li, Arnaud Le Fèvre, Yvonne Leifels, Wolfgang Trautmann, Phys. Lett. B 778, 207 (2018)
[6] P. Russotto et al., Phys. Lett. B 697-5, 471 (2011)
[7] P. Russotto et al., Phys. Rev. C 94, 034608 (2016)
[8] S. Huth, P.T.H. Pang, I. Tews, T. Dietrich, A. Le Fèvre, A. Schwenk, W. Trautmann, K. Agarwal, M. Bulla, M.W. Coughlin & C. Van Den Broeck, Nature 606 (2022)
[9] P. Russotto, M.D. Cozma, E. De Filippo, A. Le Fèvre, Y. Leifels, J. Łukasik, La Rivista del Nuovo Cimento (2023) - Review Paper